Curve Bézier

Le curve di Bézier sono un concetto fondamentale nella computer grafica e nel disegno vettoriale. Sono utilizzate per descrivere curve attraverso il controllo di punti chiamati “punti di controllo”. Queste curve sono state introdotte da Pierre Bézier negli anni ‘60 come metodo per rappresentare curve su schermi di computer. Una curva di Bézier ha la forma

$$\underline{x}(t) = \sum_{i=0}^n \underline{b}_i B_i^n(t), t\in[0,1]$$

Dove,

$$B_i^n(t) = {n \choose i}t^i(1-t)^{n-i}, i= 0,…,n$$

sono gli $n+1$ polinomi di base di Bernstein.

Nell’editor sottostante ho implementato una versione interattiva di queste curve. Gli algoritmi che ho implementato sono l’algoritmo per la computazione della curva ovvero l’ algoritmo di de Casteljau e l’algoritmo di degree elevation.

Istruzioni editor:

• 2 click con tasto sinistro per aggiungere un nuovo punto di controllo
• muovi i punti di controllo trascinandoli tenendo premuto il tasto sinistro

Warning: se non stai vedendo correttamente (o non stai vedendo) lo sketch sottostante, visita questo link. Oppure questo link per vedere e modificare il codice sorgente.

Algoritmo di de Casteljau

L’algoritmo di De Casteljau è un metodo iterativo stabile per calcolare i punti su una curva di Bézier. L’algoritmo funziona in questo modo: $$\underline{b}_i^0(t) = \underline{b}_i$$ $$\underline{b}_i^r(t) = (1-t)\underline{b}_i^{r-1}(t)+t\underline{b}_k^{r-1}(t)$$ $$k=i+1;r=1,…,n; i=0,…,n-r$$

Dove $$\underline{b}_0^n(t) = \underline{x}(t)$$ è il punto sulla curva di Bézier associato al valore del parametro $t$.

Algoritmo di degree elevation

L’algoritmo di degree elevation trasforma una curva di Bézier di grado n in una curva di Bézier di grado $n+1$:

$$\underline{x}(t)=\sum_{i=0}^n \underline{b}_i B_i^n(t)$$

$$= \sum_{i=0}^{n+1} \underline{c}_i B_i^{n+1}(t)$$

in questo modo:

$$ \underline{c}_i= \frac{i}{n+1} \underline{b}_k + \frac{n-i+1}{n+1}\underline{b}_i$$ $$k = i-1; i=1,…,n$$

$$\underline{c}_0=\underline{b}_0,\underline{c}_m=\underline{b}_n; m = n+1$$

Curve Bézier 3-dimensionali

Nell’editor sopra i punti di controllo della curva di bezier sono punti di controllo in 2 dimensioni. Ovvero, $$\underline{b}_i = { b_x \choose b_y}$$

Tuttavia tutti gli algoritmi visti sopra funzionano anche per curve tridimensionali, dove i punti di controllo avranno dunuque una componente $z$. Tutti gli algoritmi restano dunque invariati,

Warning: se non stai vedendo correttamente (o non stai vedendo) lo sketch sottostante, visita questo link. Oppure questo link per vedere e modificare il codice sorgente.

Patch di Bézier

Una patch di Bézier è definita come

$$ \underline{X}(u,v) = \sum_{i=0}^n \sum_{j=0}^m \underline{c}_{ij} B_i^n(u)B_j^m(v)$$ $$(u,v)\in[0,1]^2$$

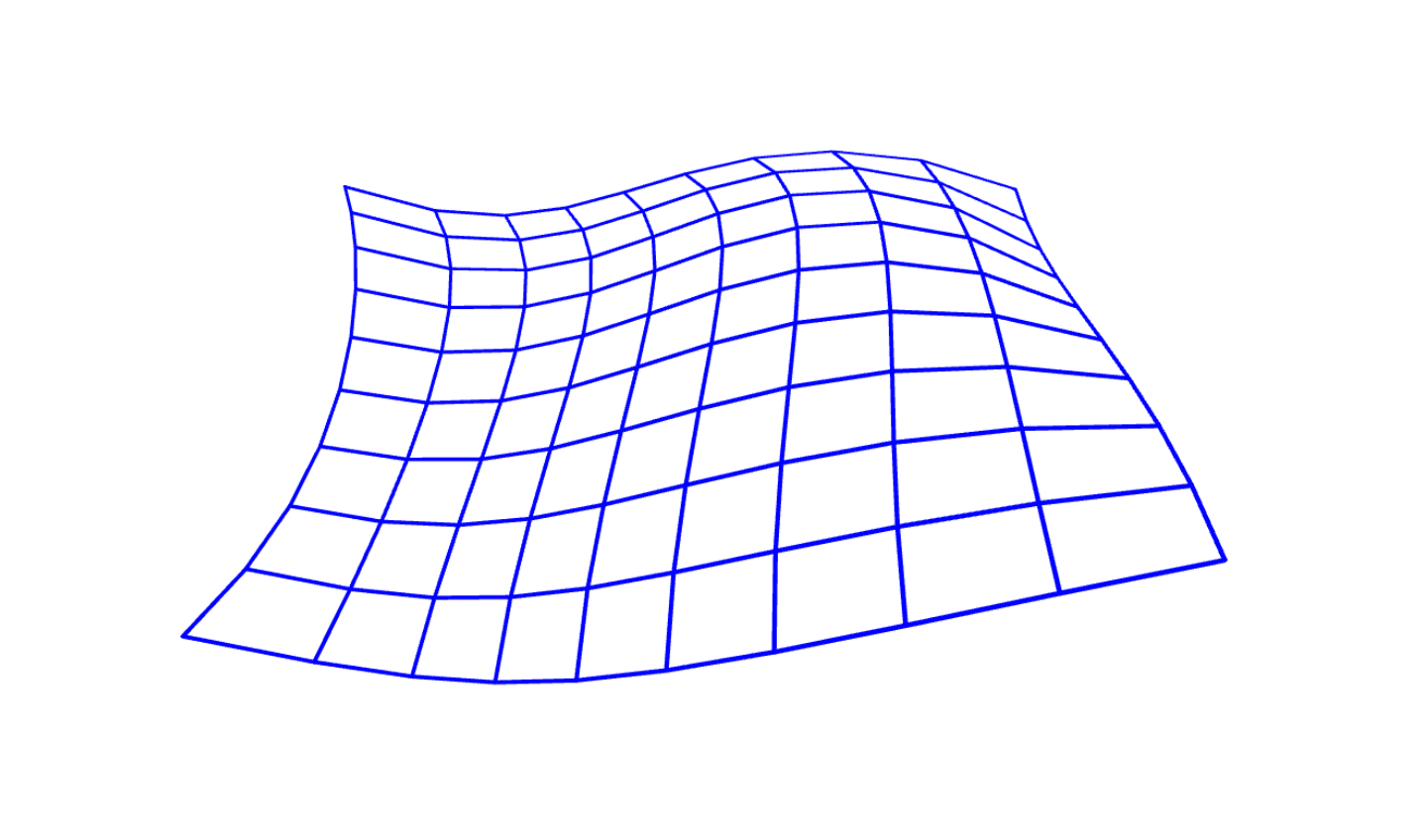
Nello skatch sottostante è visualizzata un patch di Bézier bicubico, ovvero con $m=n=3$.

Warning: se non stai vedendo correttamente (o non stai vedendo) lo sketch sottostante, visita questo link. Oppure questo link per vedere e modificare il codice sorgente.

Note sull’implementazione in p5js

Il codice è scritto con la libreria p5js ed è stato scritto con metodologia OOP. In generale tutte le versioni 2d-3d e anche Bézier patch si compongono delle seguenti classi e metodi:

class BezierCurve{
	function constructor(points: Array[Array[float]]){}
	function addControlPoint(x: float, y: float){}
	function deCastelJau(t: float){}
	function render(){
		//ConstructPoints.render() for all ConstructPoints
		//ConstructLines.render() for all ConstructLines
	}
}

class ConstructPoint{
	function constructor(x: float, y: float) {}
	function render() {}  
	function hasInside(x: float, y: float) {}
}

class ConstructLine{  
	function constructor(p1: ConstructPoint,p2: ConstructPoint) {}
	function render(){}
}

Per creare dunque una curva di Bézier è necessario istanziare una var bezierCurve = BezierCurve(points), poi sul metodo draw() di p5js richiamare il metodo render della curva in questo modo: bezierCurve.render().

Per le Bézier patch invece è stata creata una classe aggiuntiva che istanzia più classi BezierCurve.

class BezierPatch{
	function constructor(points: Array[Array[float]]){}
	function addControlPoint(x: float, y: float){}
	function render(){}
}